Queues forming during the Rush Hour
Introduction
This example discusses how it is possible to model the build up of traffic
in the rush hour, and thus to see when queues form on a straight road,
without junctions, relative to the arrival rate of cars on the section
of road.
Symbols Used
| Symbol |
Represents |
| Q(t) |
Queue length at time t |
| A(t) |
Cumulative arrivals to the queue at time t |
| D(t) |
Cumulative departures from the queue at time t |
 |
The maximum service rate |
 (t) (t) |
The service rate at time t |
 (t) (t) |
Arrival rate at time t |
Modelling the Queue
In the rush hour the arrival rate,  (t),
will rise until it reaches a maximum rate (i.e. the time when the most
people reach the point of road, when they are trying to get to work), after
this point the arrival rate will decrease. There are four main points
in this flow, as follows:
(t),
will rise until it reaches a maximum rate (i.e. the time when the most
people reach the point of road, when they are trying to get to work), after
this point the arrival rate will decrease. There are four main points
in this flow, as follows:
| Time label |
Significance |
| t0 |
The first point at which  (t)
equals the maximum service rate, (t)
equals the maximum service rate,  |
| t1 |
The point where  (t)
is a maximum (t)
is a maximum |
| t2 |
The point where  (t)
has decreased back down to (t)
has decreased back down to  |
| t3 |
The point where the queue has gone, and so  (t)
= (t)
=  (t) (t) |
The above details tend to imply that a graph of  (t)
is quadratic, and so would be differentiable twice at or near t1.
This means that
(t)
is quadratic, and so would be differentiable twice at or near t1.
This means that  (t)
has a taylor expansion about the point t1:
(t)
has a taylor expansion about the point t1:
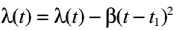 for constant
for constant  :
:
 For small t-t1, i.e. this is valid where t0 < t < t3
For small t-t1, i.e. this is valid where t0 < t < t3
This means that t0 and t2 can be estimated, by substitution:
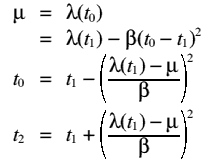
The length of the queue is the area between the curves of  (t)
and
(t)
and  (t),
i.e.:
(t),
i.e.:
.gif)
By the using similar substitutions to those used in the previous derivation
we can simplify this to:

![]() (t)
is quadratic, and so would be differentiable twice at or near t1.
This means that
(t)
is quadratic, and so would be differentiable twice at or near t1.
This means that ![]() (t)
has a taylor expansion about the point t1:
(t)
has a taylor expansion about the point t1:

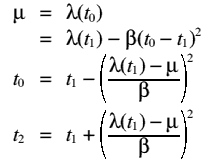
![]() (t)
and
(t)
and ![]() (t),
i.e.:
(t),
i.e.:
.gif)
