Mathematics for all Queueing Models

There is some simple mathematics which can apply to all queueing models. It is outlined below. Firstly, It is obvious from the definitions of

and

that:

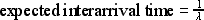
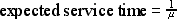
Also, generalised equations are available which apply to any queueing model:

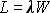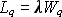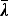It has been shown that in a steady-state queueing system, that . This is known as Little's Law, as it was discovered by John D. C. Little. A proof can be found in [LITT61]. Little also managed to show that . If the arrival rate of customers is not independent of the size of the queue, then the symbol in Little's Law can be replaced with , which denotes the average customer arrival rate over a long period of time.
If one assumes that the expected service time is as indicated as above, then it follows from the definition of W and W_q,

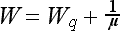
Last Updated: 14th June 1999